文章目录
好久没有更新了,最近看到博客观看数据还不错,刚好忙的事情告一段落,随手更新一篇~~
哈哈( ̄︶ ̄)

多模态的意思是,解的形态是多样的。我们以上面的图片作为例子来说明一下。可以看到,
x
1
x_1
x1? 和
x
3
x_3
x3? 对应的点目标值都是
y
1
y_1
y1?。换句话说,在目标值最优的情况下,可以找到不同的解。比如我们可以说,从长沙到北京可以找到两条长度完全一致的路,这种情况在现实世界中是经常存在的。那么推广到多目标的情况也是一样的。比如下面的图,左边是决策空间,右边是目标空间。A和B点都对应一样的目标向量P。这种情况也很好理解,比如从长沙到北京,存在路径长度和所需时间都一样的两个解。

对于决策者来说, 如果能够获得待优化问题的全部最优解, 一方面可以更深入地了解该问题, 对于刻画问题属性, 提出改进方向, 寻找最优解等具有重要作用; 另一方面, 一旦其中一个最优解因环境变化等因素导致不可用, 决策者可以方便快速地转变到另一个最优解. 对于工业生产来说, 多个最优解意味着有更多的生产方案可供选择. 在某些情况下, 决策者甚至会接受目标值稍劣的解. 例如某个解决方案要达到的加工条件较为苛刻, 或者对加工精度要求极高, 那么决策者将偏向于选择对条件要求不苛刻的解转而接受其目标函数值上的劣势.
所以说,这个问题是非常有必要去研究的。
对于绝大部分研究来说,他们的目标是获得尽可能多的最优解。这样,Pareto前沿上面的一个点,可以在决策空间中找到多个对应的解,也就是说找到 x 1 x_1 x1?和 x 3 x_3 x3?。另一个研究方向在于获得问题的全局和局部最优解集,也就是说要找到 x 1 x_1 x1?, x 2 x_2 x2?和 x 3 x_3 x3?。前期的工作(2020年以前)主要是面向第一种情况。当时也可以看到,现实中此类问题是特殊的存在,更普遍的情况应该是全局和局部同时存在。比如路径规划问题,路径长度和用时很难说完全一致,那么如果一个解路径长度和用时都比最优解差一点,但是是完全不同的路径,那么获取这个路径是有必要的。因此,现在越来越多的工作开始转向后面的情况,就是获取全局和局部的最优解集。
我们分享一篇最新的多模态多目标优化论文,也是发表在IEEE Trans on Evo Comp上,新鲜出炉,比较有意思,也已经开源了
论文地址:https://ieeexplore.ieee.org/document/9724225
[1] W. Li, X. Yao, T. Zhang, R. Wang and L. Wang, “Hierarchy Ranking Method for Multimodal Multi-objective Optimization with Local Pareto Fronts,” in IEEE Transactions on Evolutionary Computation, doi: 10.1109/TEVC.2022.3155757.
多模态多目标问题(MMOPs)通常出现在现实世界中,决策空间中的远距离解决方案具有非常相似的目标值。传统的多模态多目标进化算法(MMEAs)喜欢追求具有相同目标值的多个帕累托解决方案。然而,工程问题中更实际的情况是,一个解决方案在目标值上比另一个稍差,而解决方案在决策空间中相距甚远。换句话说,这类问题有全局和局部的帕累托前沿。在这项研究中,我们提出了几个具有多个局部帕累托前沿的基准问题。然后,我们提出了一种带有层次排位法的进化算法(HREA),以根据决策者的偏好找到全局和局部的帕累托前沿。关于HREA,我们提出了一种局部收敛质量评价方法,以更好地保持决策空间的多样性。此外,还引入了一种层次排位法来更新收敛档案。实验结果表明,与其他最先进的MMEA相比,HREA在解决所选基准问题方面具有竞争力。
论文作者在文献中提出了一个包含有局部和全局最优解集的测试集(IDMPe),部分测试问题的PF和PS如下所示

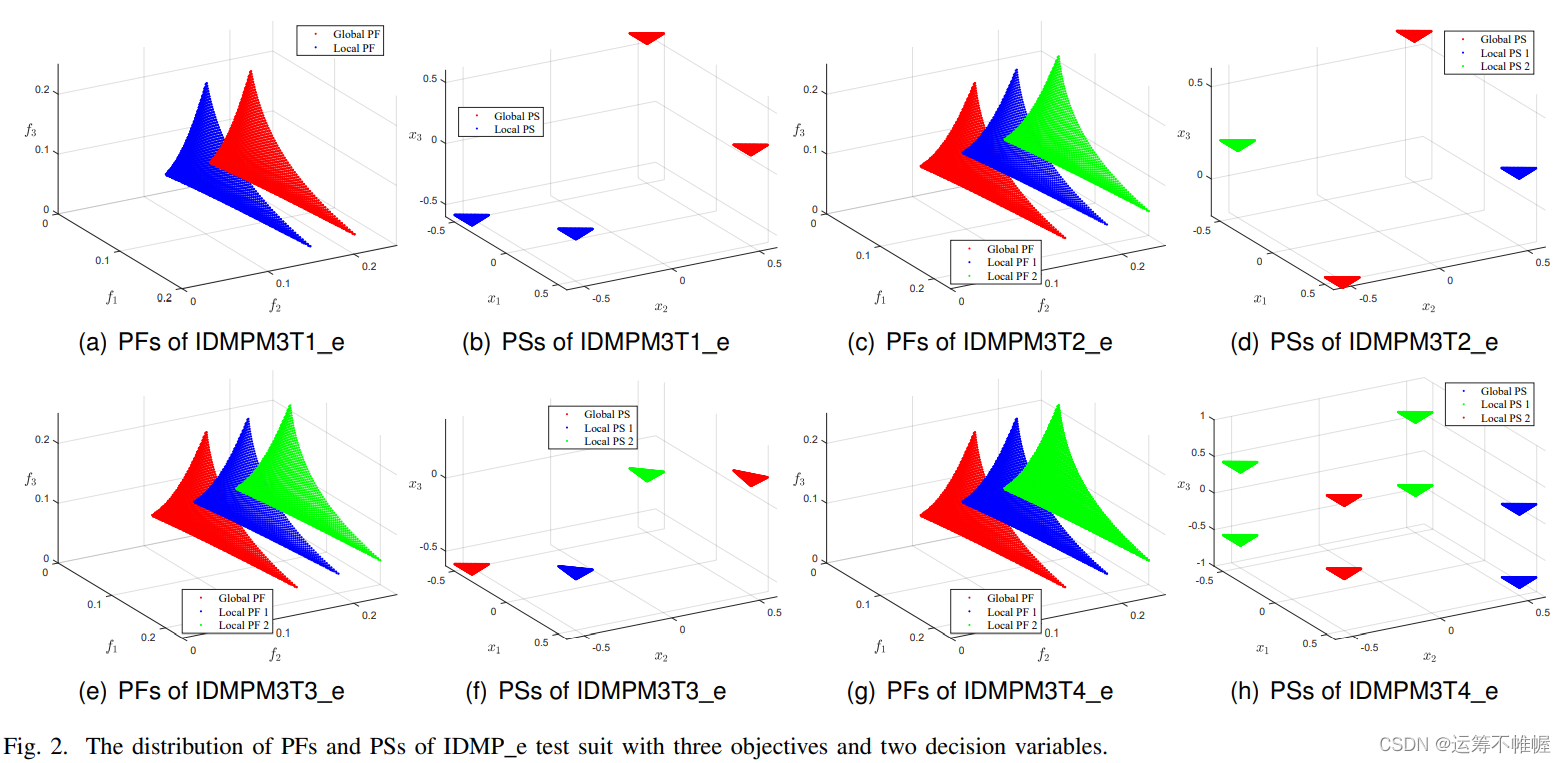
可以看到,测试问题里存在多个全局和局部最优。
基于此类问题,作者提出了一种分层选择的策略。算法流程如下:



思路也很简单,收敛档案的更新过程在算法3中进行了说明。主要任务是维护两个种群,即 P i c k e d P o p PickedPop PickedPop和 R e m a i n P o p RemainPop RemainPop。首先,选择非支配性的解决方案来形成全局PF(第2-3行)。然后,删除 R e m a i n P o p RemainPop RemainPop中与 P i c k e d P o p PickedPop PickedPop中的任何解决方案接近的解决方案(第7行)。这样做的原因是,如果一个方案在决策空间中与 P i c k e d P o p PickedPop PickedPop中的任何方案接近,那么它们在目标空间中也可能接近。在这种情况下,层次排位法将这个方案视为下一个PF层。当 R e m a i n P o p RemainPop RemainPop不是空的时候,我们首先拾取 R e m a i n P o p RemainPop RemainPop的PF,称为 N e x t P o p NextPop NextPop。然后,如果 N e x t P o p NextPop NextPop中存在一个不可接受的解决方案( M a x F > 1 MaxF>1 MaxF>1),那么我们就终止循环。否则,如果 N e x t P o p NextPop NextPop中的所有解决方案都是可接受的,那么我们将 N e x t P o p NextPop NextPop加入到 P i c k e d P o p PickedPop PickedPop中,并在 R e m a i n P o p RemainPop RemainPop中删除它们;
作者贴心的开源了代码:
https://github.com/Wenhua-Li/HREA
现在来说,该领域存在比较严重的问题如下:
考虑局部PS可以大大增强算法在保持多样性方面的能力,例如DNEA-L、MMOEA/DC和HREA。然而,目前考虑获得局部PS的工作很少。IEEE CEC 2019和CEC 2020多模态优化竞赛在提高局部MMOPs的关注度方面做出了一些努力。此后,MMOEA/DC和HREA被提出。在MMO社区,开发获得局部PS的算法是一个更实用的大方向。
对于一个给定的问题,缺乏一个多模态的检测方法。也就是说,对于决策者处理某个现实世界的问题,没有关于这个问题是否是MMOP的信息。根据以前的一些工作,MMEAs的收敛能力比最先进的MOEAs差。因此,MMEAs不会成为第一选择。开发一种有效和高效的工具或方法来检测问题的多模性是非常重要和紧迫的。另一方面,由于MMEAs专注于提高决策空间中解决方案的多样性,在目标空间中的收敛能力肯定比普通MOEAs差。因此,对于一个不确定是否是MMOP的问题,DM会缺乏选择MMEA的信心。到目前为止,平衡收敛性和多样性仍然是MMO社区的一个具有挑战性和紧迫性的研究课题。
到目前为止,所有测试问题都是连续的,很少有研究分析离散的或混合决策变量的MMOPs。CEC2021多模态多目标路径规划优化也曾在丰富离散优化领域方面做了一些努力。对于许多现实世界的问题,决策变量的类型通常是多种多样的,例如,连续的、离散的和二进制的。尽管将现有的测试套件转化为离散优化问题很容易,但目前还没有工作系统地分析现有的MMEA在混合决策变量问题上的性能。
现有的MMEAs在解决有许多决策变量的MMOPs时面临巨大的挑战。许多提议的MMOPs的求解相对简单,例如MMF1-8。一个重要的原因是,对于多维度的问题,不能直接观察到多个PS。因此,现有的测试套件无法准确评估搜索能力和效率。此外,利用保持多样性的技术作为第一选择策略的缺点还没有得到很好的研究。MMOP社区需要一个全面的MMOP测试套件,在搜索PF方面有困难。